12/26/06
The material explained here is conceptually at a higher level than the earlier tutorials; it also covers relatively rare cases.
To understand the concepts of scope, free, bound, and free for. To learn of the restrictions on the quantificational rules
The new predicate rules of inference using quantifiers have restrictions on them which are expressed in terms of these concepts. And, in turn, the restrictions on the rules allow them to be used properly.
There is a rule of derivation-- Universal Instantiation-- which, roughly speaking, allows you to do the following... if a formula has a Universal Quantifier as its main connective you may remove the Universal Quantifier and have as a new line the body of the formula with a term substituted in for all free occurrences of the variable of quantification within the scope. For example,
5 (x)Fx 6 Fa 5 UI
5 (x)Fx 6 Fb 5 UI
5 (x)Fx 6 Fy 5 UI
are all proof fragments illustrating Universal Instantiation.
There is a restriction on the rule, but to understand the restriction you need to understand the concepts which are used to express it.
Notice the form of a formula with a quantifier as its main connective. Examples of such formulas are (x)(Fx), (∃x)(Fx.Gx), (x)(Fx⊃Gx). In each case there is the quantifier with its variable, enclosed within brackets, and this is followed by a formula known as the scope of the quantifier. In our examples, (Fx) is the scope of the first one, (Fx.Gx) the scope of the second, and (Fx⊃Gx) the scope of the third.
More formally...
If <scope> is any well-formed formula then (<variable>)<scope> is the universal quantification of <scope> using <variable> and (∃<variable>)<scope> is the existential quantification of <scope> using <variable> . In each case the <scope> is the scope of the quantification.
The notion of the scope of a quantifier is important; and it is good practice to enclose the scope in brackets so as to display exactly what it is. For example, the scope of the formula (x)Fx⊃Gx is Fx not (Fx⊃Gx); the formula as a whole will be read as ((x)(Fx))⊃Gx; such a formula is better written as (x)(Fx)⊃Gx.
A quantifier binds all occurrences of its <variable> in its scope. An occurrence of a variable which is not bound is called free. So, in (x)(Fx)⊃Gx the occurrence of x immediately after F is bound whereas the occurrence of x immediately after G is free; but in the formula (x)(Fx⊃Gx) both occurrences are bound.
Substitutions are on occasions made of one term for free occurrences of another-- in Universal Instantiation, for example.The notation
<wff>[<newterm>/<oldterm>] means the formula <wff> with <newterm> substituted for the free occurrences of <oldterm> throughout.
So, for example, (Fx⊃Gx)[a/x] is (Fa⊃Ga).
There is an obstacle to successful substitution, and that is capturing. Say we have a formula (x)(∃y)Lxy ('everybody loves somebody', perhaps) and we start taking instantiations of the universal quantifier by removing it to obtain the scope (∃y)Lxy and substituting terms for the free x ; thus, (∃y)Lay ('a loves somebody') (∃y)Lby ('b loves somebody'), this is fine and all these instantiations follow from the original statement but if we try to substitute y for x we get (∃y)Lyy ('somebody loves themself') which does not follow; the occurrence of x within the scope of the y quantifier is not free for the substitution y; such a substitution leads to capturing.
Capturing motivates the following definitions. Any term occurs within itself. A variable x is free for term t in formula F iff there is no free occurrence of x in F within the scope of a quantifier whose variable of quantification occurs in t. (Sometimes a different phrase is used for 'free for' alternatively it is sometimes said that a substitution is legitimate.)
Sounds terrible, doesn't it? But suppose F is
(Gxy .~(∃y)(Lxy))⊃((z)((Rx.Sz) ≡ (∃x)(Lxw))
and the variable x is our interest;
so, as examples, x is free for a in F, x is free for w in F, x is free for x in F, but x is not free for y in F, but x is not free for z in F.
The full rule of Universal Instantiation needs to take account of capturing.
If a derivation contains a line of the form
n (<variable>)<scope> <any justification>
then a line of the form
<<scope>[<term>/<variable>]> 'n UI'
may be added to the derivation, provided that <variable> is free for <term> in the <scope> ie that the substitution [<term>/<variable>] is legitimate .
Universal Generalization allows universal generalization on a variable, permitting steps illustrated by the following proof fragments.
5 Fx 6 (x)Fx 5 UG
5 Fy 6 (x)Fx 5 UG
but obviously the inference from one thing, x or y, being, say, F, to all of them being F is not in general valid. Previous lines to a fragment like one of these are often something like
3 (x)(Fx.Gx) 4 Fx.Gx 3 UI 5 Fx 4 Simp 6 (x)Fx 5 UG
This inference, as a whole, is perfectly good. We need to pay attention to where the variable quantified on, the x in Fx of line 5, has come from. If it has come from UI, that is fine.
There are three other possibilities. It might have been among the original premises of the proof. For example, in a different proof line 4 might have been one of the premises. This is fine also. Free variables among the premises are not in general a good thing. They are something of a stylistic aberration. This is because we talk about validity in terms of the truth of the premises and the truth (or falsity) of the conclusion. But formulas with free variables are not either true or false so immediately the notions of validity and invalidity do not apply. But contrary to our good intentions, mathematicians regularly start proofs with a set of premises including one like
x + y = y+ x
Fortunately they do not understand this statement as really being a free variable form. Instead they use it as shorthand for
(x)(y)(x + y = y+ x)
In other words, formulas with free variables among the premises are understoods as being implicitly universally quantified.
A second possibility for the origin of the variable quantified on is that the x has come from Existential Instantiation. For example
3 (∃x)(Fx.Gx) 4 Fx.Gx 3 EI 5 Fx 4 Simp 6 (x)Fx 5 UG
This is an invalid inference-- it does not follow from there being one thing that is F and G that all things are F. We need a restriction here on UG.
The variable quantified on, x, must not appear free in any previous line obtained by Existential Instantiation EI.
The third possibility is Conditional Proof. There might be proof fragments like
-> n. Gx AP ? ? << G⊃F ?
or
-> n. Gx AP
<proof fragment in here> ?
Fx ? ? ? << Gx⊃Fx ?
or
-> n. Gx AP
<proof fragment in here> ? k
Fx ?
Gx⊃Fx k ⊃I
In one sense, the 'additional premises' of conditional proofs are premises like any other, so it might be in order to let them have free variables understanding those to be univerally quantified. But the cleanest move is just to ban them from UG. Thus the second restriction on UG is
The variable quantified on, x, must not appear free in any undischarged 'Assumed Premise' (of an open conditional proof).
The full rule for UG is:
If a derivation contains a line of the form
n. <formula>[<variable2>/<variable1>]> <any justification>
then a line of the form
(<variable1>)<formula> 'n UG'
may be added to the derivation, <variable1> may be the same or different to <variable2>, provided that
a) <variable2> does not appear free in any previous line obtained by EI,
b) <variable2> does not appear free in any undischarged 'Assumed Premise' (of an open conditional proof).
This rule is almost correct as it was originally stated. We just need to be sure that no 'capturing' occurs on the backstep. Our notation thus far permits the following
5 (∃y)Fyy 6 (∃w)(∃y)Fwy 5 EG
Here 'y' is the <term> and 'w' the <variable> and line 5 is the scope of line 6 with y substituted for free w. But we don't want this inference. We just need to rephrase the rule to make the substitution legitimate (ie to avoid capture). The result is
If a derivation contains a line of the form
n. <formula>[<term>/<variable>]> <any justification>
where <variable> is free for <term> in <formula> ie the substitution is legitimate
then a line of the form
(∃<variable>)<formula> 'n EG'
may be added to the derivation, provided that <variable> is new to <formula>.
This rule is fine as it is.
The Interpretation in Predex14 shows an Interpretation similar to this

if it does not draw a similar one for yourself.
Proofs
The rule Universal Instantiation has the restriction on it that the proposed instantiation should not result in capturing (in the terminology... the variable of instantiation must be free for the term of instantiation in the scope).
So, for example,
(x)(∃y)Rxy ∴ (∃y)Ray
(x)(∃y)Rxy ∴ (∃y)Rby
(x)(∃y)Rxy ∴ (∃y)Rxy
(x)(∃y)Rxy ∴ (∃y)Rzy
are all valid arguments (and may be proved so by one use of Universal Instantiation). Derive them.
But
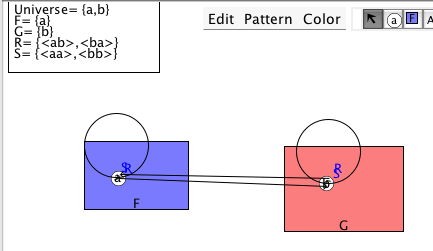
(x)(∃y)Rxy ∴ (∃y)Ryy
is invalid. Look at the interpretation of the diagram below and note that all the premises are true and the conclusion false at one and the same time. This argument cannot be proved to be valid (for it is not). But the unwary might think that they can prove it by one use of Universal Instantiation which plugs in y (but this is the forbidden case where the y gets captured by the other quantifier).
Proofs
The rule Existential Generalization has the restriction on it that no occurrence of the term that you are generalizing on is bound by another quantifier. In other words, working back from the result back substitution should not result in capturing (in the terminology... the variable of generalization must be free for the term of generalization in the scope).
So, for example,
(x)Sxa ∴ (∃y)(x)Sxy
(x)Sxb ∴ (∃y)(x)Sxy
(x)Sxy ∴ (∃y)(x)Sxy
(x)Sxz ∴ (∃y)(x)Sxy
are all valid arguments (and may be proved so by one use of Existential Generalization). Derive them.
But
(x)Sxx ∴ (∃y)(x)Sxy
is invalid. Look at the interpretation of the diagram and note that all the premises are true and the conclusion false at one and the same time. This argument cannot be proved to be valid (for it is not). But the unwary might think that they can prove it by one use of Existential Generalization which generalizes on one occurrence of x (but this is the forbidden case where the occurrence is already quantified by another quantifier-- back substituting the x leads to it getting captured by the other quantifier).