Browser Menus
File menu
New browser produces a new viewer with the four panes looking at the journal, the proof, the tree, and the interpretation.
New file produces a new journal, proof, tree and interpretation within the existing browser. If there is an old document there, which has not been Saved, the User is prompted to Save it.
Open file opens an existing document within the present browser. If there is an old document already on display there, which has not been Saved, the User is prompted to Save it. Open can open many types of document. It will open documents produced by Deriver, restoring the journal, proof, tree, and interpretation. It will open HTML documents, such as Web pages, into the journal. And it will open many kinds of text documents into the journal.
Close browser closes the foremost browser. If there is a document already on display there, which has not been Saved, the User is prompted to Save it. If the browser is the only or last browser on display, the application as a whole will exit.
Save, and Save As are standard. They save all three of the journal, proof, tree, and interpretation.
Save Journal As HTML does exactly that (but the proof and interpretation are not saved). Saving this way allows the Journal to be opened elsewhere either as a Web page or, for example, in WORD.
Exit exits or quits the entire program. The User is prompted to Save any unsaved documents
Help Menu
About ...
Preferences allows the running application to be configured.
[As preferences are changed, what Deriver presents can also change, sometimes considerably. Most obviously, systems with extra rules of inference (for example, modal logic, set theory, theories with identity, etc. will add the relevant extra rules) then, for example, were a true 'modal' to be reset to false the modal rules would be removed. There can also be some not so obvious changes. For example, the Wizard Menu often has Derive It and Next Line menu items, these depend on a theorem prover which does the proof for you then produces it (or parts of it) at your request. But, for example, no theorem prover is available for set theory (with its axiom of induction), and none is available for modal logics, nor for identity. So, if the system starts running set theory (or modal logics, or with identity, etc.) the Derive It and Next Line items will no longer appear under the Wizard Menu.]
The preferences dialog opens to display
You select which Preference you wish to set, that will load its 'Key'. You then enter the 'Value' you want, and Press 'Put Key= Value'. That will set that preference, and changes will take place on all new and subsequent Browsers. (In the displayed image the 'colorProof' preference has been chosen, but no new value set for it.)Home [default not set] shows or chooses the Directory that Deriver opens in. In general, there is probably not a lot of reason to be changing this by hand. When you Open or Save a file the standard Open/Save dialog will allow you to navigate to wherever you wish to be and Deriver will automatically remember where your last Save was. If you never do any Saves, and you wish to Open from somewhere other than the default, use this Preference to set your choice.
User [default=""] is typically for lab or classroom use, where there are many Users, setting this identifies which student or User did the work.
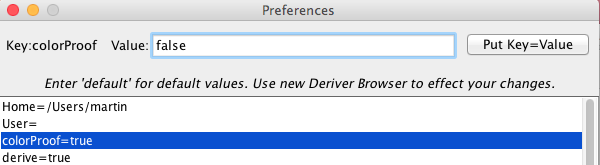
colorProof [default=true] shows the subproofs, or indents, in different colors (red, blue, green, etc.). To give an example of changing a preference, this would be changed by selecting colorProof and typing in 'false'
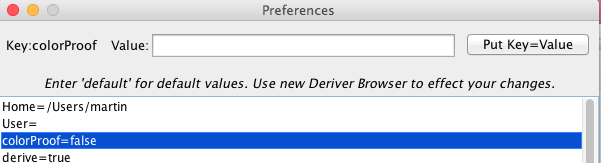
then pressing 'Put Key=Value' and the result will be
derive [default=true], enables the theorem prover which will do the derivations for you (off the Wizard menu).
endorseMenuItem [default=true], enables the Endorse-Deny items off the Semantics Menu. This allows the User to play the Endorse-Deny game which is an elementary form of game-theoretic semantics.
firstOrder [default=false], enables First Order theories, such as arithmetic. Such theories often have constants of their own e.g. 0 (zero) and 1 (one), functions such as + (plus) which can be written infix (e.g. 1+1 not Plus(1,1)), and equality =. So, with firstOrder set to true, Deriver will parse, say, 0+1=1 and F(0+1') as being well-formed formulas, and you can do proofs with such formulas (extra rules, such as Induction, will be available).
gamesMenu [default=true], displays a Games menu.
htmlMenu [default=true], displays an HTML editing menu.
identity [default=false], if this is set true then formulas like a=b will be parsed as being well-formed and there will be extra rules of inference to permit derivations like F(a), a=b ∴ F(b).
interpretations [default=true], enables the drawing window and 'interpretations' for semantics.
lambda [default=false], enables the lambda calculus and its rules.
modal [default=false], enables modal logics and their rules.
paletteText [default=logicSystemDefault], allows you to set the Palette text. The Palette is the small collection of symbols at the top of the journal (for your use in Proofs etc.). The default is that the Palette displays symbols suitable for the system you are using, for example & (for and) in one system and ^ (for and) in a different system, and modal symbols for modal, lambda symbols for lambda, etc. But, actually, you can have whatever you like, either special symbols, reminders, mottos, whatever. Just set the paletteText to, say, "Now is the winter of our discontent" and that is what will be on your palette.
parser [default=default], allows you to set the Parser (i.e. the logic system that Deriver will run). The display will look something like
default [barwise bergmann copi gentzen hausmann herrick howson priest]
the first entry, in this case 'default', is the logic system that Deriver is running. [Another example, in the image above the system is running 'barwise']. The other labels within the square brackets are the choices available to you, in this case
[barwise bergmann copi gentzen hausmann herrick howson priest]
So, if you wanted to run a 'priest' system, you would just type in priest as the value and Press 'Put Key= Value'. Which parser is running matters, for example Fa is well-formed in some systems but not in others (other systems might use F(a) as the syntax for that formula). There is a small 'gotcha' here. If you create and save some files in one system, say Gentzen, then change parser to, say, Hausmann, then try to open your Gentzen files with a Hausmann system, your files might not open with full information (the system will skip any formulas that are not well formed and your Gentzen formulas might not be well-formed under a Hausmann system).
proofs [default=true] enables the Proofs windows (in some settings Users might want to do Trees only, in which case they would set this false).
readFromClipboard [default=false] enables direct reading from the Clipboard. You can, of course, copy something and paste it in to the Journal etc.. But this speeds that process up. If it is enabled, you can select some text from anywhere, copy it (which copies it to the Clipboard), then Start a Proof, Start a Tree etc. and Deriver will read its input directly from

the Clipboard.
rewrite [default=true] enables the rewrite rules.
rightMargin [default=340] sets the right margin.
setTheory [default=false] enables set theory, so for example x ∈ y is well formed, and there are additional rules of inference.
simpleFileMenu [default=false] disables many choices on the File Menu to make the presentation easier for beginning students.
trees [default=true] enables the tree panel for tree proofs.
typeLabels [default=false] enables type labels.
useAbsurd [default=false] enables the use of Absurd. When doing a Reductio ad Absurdum proof, the proof is trying to derive a contradiction, say two formulas A and ~A. Sometimes this is easier to understand by having a propositional constant 'Absurd' which is defined as being A&~A (for any formula -A), then a reductio proof makes an assumption then tries to derive Absurd from it.