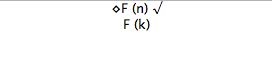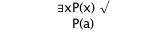default

6/1/12

Reading

A text like

Rod Girle [2000] Modal Logics and Philosophy

would definitely be a help here.

Tutorial

[Modal logic is a vast area, what is being presented here is the briefest of glimpses through the shop window (a book like the Girle would help you go further).]

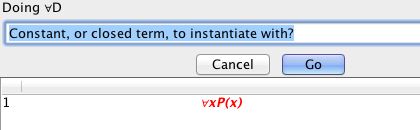
In modal logic, there are the additional symbols □ (necessary) and ◊ (possible) and, in the background, the notion of 'possible worlds'.

Last altered 6/20/12

A central use for Trees is to produce a counter example to an invalid argument. To do this, you construct a tree with a complete open branch. You will be able to do this for invalid arguments (but not valid ones). Then you run up that branch assigning all atomic formulas True and all negations of atomic formulas False.

 

This software will let you try a few.

 

---

 

Exercise: Finding a counter-example.

 

6/20/12

You need to know some propositional logic to be able to understand the tree tutorials to come. In particular, you need to know about the symbols used in propositional logic, truth tables, satisfiability, consistency, and semantic invalidity (by counter example). You do not need to know propositional rules of inference and derivations.

Howson [1997] will give you enough background.

Alternatively you could look at the first five propositional tutorials in Easy Deriver

6/2/12

Review of Tree Propositional Rules, shown as patterns

Here the letters 'P' and 'Q' are being used to stand for entire well formed formulas (so, on a particular occasion,  'P' might stand for the atomic formula 'F' and, on another occasion, it might stand for the compound formula 'F&G').

6/3/12

You can try your own exercises here.

Here are a few hints

• You have to use the right (unicode/html) logical symbols. Check Writing symbols
• The symbols in use here are ~ & ∨ →  

  ≡

---

 

∃D. The constant, a, must be new to the branch [here the computer will choose for you]

 

---

 

∀D. Any closed term, stage 1, your choice

∀D. Any closed term, stage 2, the constant 'a' chosen

---

 

¬∃D.

6/6/12

Reading

[These might help, you need only scan them.]

K.H.Blasius et al. eds.[1990] Sorts and Types in Artificial Intelligence
Maria Manzano [1996] Extensions of First-Order Logic
John Sowa [2000] Knowledge Representation

6/5/12

Tutorial

Set theory is an extensive topic introduced elsewhere. It can be written as a first order theory.

There is one axiom schema, Abstraction (or Comprehension), which can generate infinitely many axioms

∀y(yε{x:Φ[x]}≡Φ[y])

Axiom Schema of Abstraction (or Specification or Comprehension). The Set Builder Axiom Schema.

And a number of other axioms

 (x=y) ≡∀z(zεx≡zεy))      Axiom of Extensionality