2013
Reading
Colin Howson, [1997] Logic with trees Chapter 11
Tutorial
Set theory is an extensive topic introduced elsewhere. It can be written as a first order theory.
There is one axiom schema, Abstraction (or Comprehension), which can generate infinitely many axioms
∀y(yε{x:Φ[x]}↔Φ[y])
Axiom Schema of Abstraction (or Specification or Comprehension). The Set Builder Axiom Schema.
And a number of other axioms
(x=y) ↔∀z(zεx↔zεy)) Axiom of Extensionality
(x⊂y) ↔∀z(zεx→zεy) Axiom of Subsets
∀x(x∉∅) Axiom of Empty Set
∀x(xεU) Axiom of Universe Set
zε(x∪y) ↔ (zεx∨zεy) Axiom of Union
zε(x∩y) ↔ (zεx∧zεy) Axiom of intersection
zε(x-y) ↔ (zεx∧z∉y) Axiom of Complement
zε{x,y} ↔ (z=x∨z=y) Axiom of Pair
zε ℘(x) ↔ (z⊂x) Axiom of Power Set
[These axioms would normally be presented as universally quantified closures ie with leading ∀x∀y etc.]
Then these can be taken as the starting formulas for trees, and the result would be first order (naive) set theory.
Set theory uses many definitions. Trees can accommodate these (but the trees would get a little large and elaborate). We will pass on this.
However there certainly is one theorem worth proving ...
Russell's Paradox.
(Naive) set theory is inconsistent, as was discovered by Bertrand Russell. The problem lies with the Schema of Abstraction, then all that is needed is to consider the set of those objects which are not members of themselves. This seems to be a perfectly good defining property for a set (most sets seem to be not members of themselves; for example, the null set ∅ is not a member of ∅ ie ∅∉ ∅). But if we give this set a name, say b, and ask if b is a member of itself: it is iff it isn't (which is a contradiction).
∀y(yε{x:Φ[x]}↔Φ[y]) Axiom Schema of Abstraction (or Comprehension)
b={x:x∉y}
So you need to show that
∀y(yε{x:x∉y}↔y∉y), b={x:x∉y} are inconsistent, and that can be done by closing a tree for them
Here's (more than) a hint.
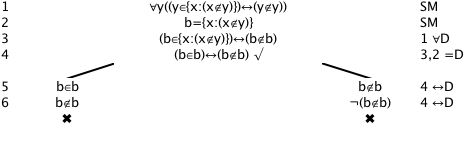
This inconsistency or paradox ruins (naive) set theory.
If you decide to use the web application you can launch it from here Deriver [Howson] — username 'logic' password 'logic'. Then either copy and paste into the Journal or use the Deriver File Menu to Open Web Page with this address https://softoption.us/test/treesStandAlone/howson/CombinedTutorialsHowson.html . Then select the desired formula(s) and Start Tree off the Actions Menu.
Preferences
You will need to set some Preferences for this. Set identity to true (and that will give you the identity rules) set firstOrder to true (to get first order theories), set setTheory to be true (for set theory); and you can check that the parser is set to Howson.