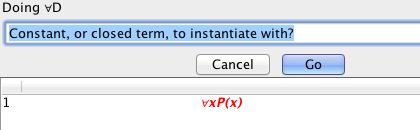
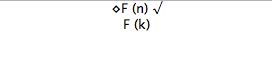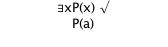Tree Tutorial 8 Modal Trees
1/31/20
Reading
Colin Howson, [1997] Logic with trees Chapter 12 Section 2
The Howson [1997] does not expand on modal logic (and modal trees) so a text like
Rod Girle [2000] Modal Logics and Philosophy
would definitely be a help here.
Tutorial
[Modal logic is a vast area, what is being presented here is the briefest of glimpses through the shop window (a book like the Girle would help you go further).]