2013
The Tutorial
Existential Instantiation permits you to remove an existential quantifier from a formula which has an existential quantifier as its main connective. It is one of those rules which involves the adoption and dropping of an extra assumption (like ∼I,⊃I,∨E, and ≡I).
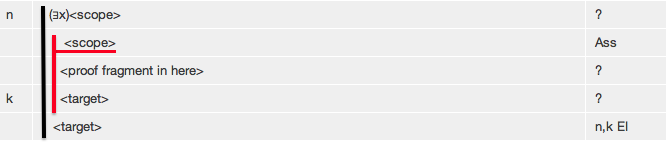
The circumstance that Existential Instantiation gets invoked looks like this.

That is, a formula you have has an existential quantifier as its main connective-- and you are trying to obtain some formula which we will call <target>.
For example,

invites the use of EI. In this case (∃x)(Fx) is the existential formula, (Fx) is its scope, and (∃y)(Fy) is the target.
To use EI you follow a three stage process. First you assume the <scope>. The illustrated fragment will then become

Second you continue deriving in this new context until you manage to derive <target> thus

Finally you select <target> at the end of the sub-proof, select the existential formula, and click EI to complete the existential instantiation.
In the example, the derivation would look like

There are restrictions on EI. The variable of quantification must not be free either
- a) in the <target> ,
- or b) in the assumptions of the final <target> line,
- or c) in the assumptions of the existential formula that EI is used on.
More about these later.
Exercise to accompany Predicate Tutorial 11.
Exercise 1 (of 3)
It is probably easier to learn EI using Tactics. After you start each derivation,switch Tactics on, select the existentially quantified formula, and click EI.
Derive the following
a) (∃x)(Fa) ∴ Fa
b) (∃x) (Fx∧Gx) ∴ (∃x)(Fx )
c) (∃x) (Fx∧Gx) ∴ (∃y)(Gy)
d) (∃x)(Fx)∴ (∃y)(Fy)
e) (∃x)(Fx∧Gx) ∴ (∃y)(Fy)∧(∃z)(Gz)
Exercise 2 (of 3)
Repeat the derivations of Exercise 1 without using Tactics.
a) (∃x)(Fa) ∴ Fa
b) (∃x) (Fx∧Gx) ∴ (∃x)(Fx )
c) (∃x) (Fx∧Gx) ∴ (∃y)(Gy)
d) (∃x)(Fx)∴ (∃y)(Fy)
e) (∃x)(Fx∧Gx) ∴ (∃y)(Fy)∧(∃z)(Gz)
Exercise 3 (of 3)
Each of following derivations will use Existential Instantiation at some stage.
Derive
a) ∴ (∃x)Fx≡(∃y)Fy
b) (∀x)Fx,(∃x)~Fx∴G
c) ∴ (∃x) (Fx∨Gx) ≡ (∃y)Fy∨(∃z)Gz
d) (∃x)(Fx∨Gx),(∀x)(Fx⊃Hx),(∀x)(Gx⊃Hx)∴(∃x)Hx
e) ~(∃x)(Fx∧~Gx),~(∃x)(Gx∧~Hx)∴(∀x)(Fx⊃Hx)
f) ~(∃x)Gx,(∀x)(Fx⊃Gx)∴(∀x)(Fx⊃Hx)
g) (∃x)Fx∨(∃x)Gx,(∀x)((Fx∨Gx)⊃Hx)∴(∃x)Hx